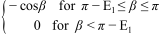Appendix 2 - The Methodology for the Minimum Power Assessment
Clasification Society 2024 - Version 9.40
Statutory Documents - IMO Publications and Documents - Circulars - Marine Environment Protection Committee - MEPC.1/Circular.850 Rev.3 - Guidelines for Determining Minimum Propulsion Power to Maintain the Manoeuvrability of Ships in Adverse Conditions - (7 July 2021) - Appendix 2 - The Methodology for the Minimum Power Assessment

Appendix 2 - The Methodology for the Minimum Power Assessment

 1 Minimum Power Assessment is based on the solution of a one degree-of-freedom manoeuvring equation in longitudinal direction to demonstrate that the ship can move with the speed of 2.0 knots through water in wind and wave directions from head to 30 degrees off-bow for a situation of weather vaning. The assessment consists of the following steps:

  • .1 calculate the maximum total resistance in the longitudinal ship direction over wind and wave directions from head to 30 degrees off-bow;

  • .2 calculate corresponding required brake power and rotation speed of the installed engine, considering the resistance and propulsion characteristics of the ship including appendages; and

  • .3 check whether the required brake power does not exceed the maximum available brake power of the installed engine, defined according to the engine manufacturer data at the actual rotation speed of the installed engine.

2 The maximum total resistance is defined as sum of the resistance in calm-water at the 2.0 knots forward speed U and the maximum added resistance in seaway Xa over wind and wave directions from head to 30 degrees off-bow.

Requirement

3 To satisfy the requirements of Minimum Power Assessment, the required brake power in the adverse conditions at the forward speed 2.0 knots through water should not exceed the available brake power of the installed engine in the same conditions:

≤

4 The required brake power is calculated as

  • where

  • nP (1/s) is the propeller rotation rate in the specified adverse conditions and the specified forward speed;
    Q (N⋅m) is the corresponding propeller torque;
    ηs is the mechanical transmission efficiency of the propeller shaft, approved for the EEDI verification;
    ηg is the gear efficiency, approved for the EEDI verification; and
    ηR is the relative rotative efficiency.

5 The available brake power in the adverse conditions at the forward speed is defined as the maximum engine output at the actual rotation speed, taking into account maximum torque limit, surge/air limit and all other relevant limits in accordance with the engine manufacturer's data.

Definition of propulsion point

6 The propeller rotation rate nP and the corresponding propeller advance ratio J in the adverse conditions at the forward speed are defined from the propeller open-water characteristics by solving the following equation:

  • where

  • KT is the thrust coefficient of the propeller, defined from the propeller open-water characteristics;
    T (N) is the required propeller thrust;
    ρ (kg/m3) is the sea water density, ρ = 1025 kg/m3;
    ua (m/s) is the propeller advance speed; and
    DP (m) is the propeller diameter.

7 The corresponding torque of the propeller is calculated as

  • where

  • KQ is the torque coefficient of the propeller, defined from the propeller open-water characteristics.

8 The propeller advance speed ua is calculated as

  • ua = U(1 − w)

  • where

  • U (m/s) is the forward speed 2.0 knots through water; and
    W is the wake fraction.

Definition of required propeller thrust

9 The required propeller thrust T is defined from the equation

  • where

  • Xs (N) is the resistance in calm-water at the forward speed including resistance due to appendages;
    Xa (N) is the maximum added resistance in seaway Xa; and
    t is the thrust deduction factor taking into account suction force on the ship hull due to propeller thrust.

Definition of calm water characteristics

10 The calm-water characteristics used for the assessment, such as calm-water resistance, self-propulsion factors and propeller open-water characteristics, are defined by the methods approved for EEDI verification, including:

  • .1 the calm-water resistance Xs, defined from the following equation:

    Xs = (1 + k)CF1ρSU2

    where k is the form factor, CF is the frictional resistance coefficient, ρ is sea water density, ρ = 1025 kg/m3, S is the wetted surface area of the hull and the appendages and U is the forward speed;

    .2 the thrust deduction factor t and wake fraction w at the forward speed and relative rotative efficiency ηR. Default conservative estimate may also be used for thrust deduction factor and wave fraction; t=0.1 and w=0.15 respectively; and

    .3 the propeller open-water characteristics KT(J) and KQ(J).

Definition of added resistance

11 The maximum added resistance in seaway Xa is defined as sum of maximum added resistance due to wind Xw, maximum added resistance due to waves Xd and maximum added rudder resistance due to manoeuvring in seaway Xr over wind and wave directions from head to 30 degrees off-bow.

Definition of wind resistance

12 The maximum added resistance due to wind Xw is calculated as

  • where

  • is the non-dimensional aerodynamic resistance coefficient;
    ε (degree) is the apparent wind angle;
    ρa (kg/m3) is the air density, ρa=1.2 kg/m3;
    vwr (m/s) is the relative wind speed, vwr=U + vwcosμ;
    vw (m/s) is the absolute wind speed, defined by the adverse conditions in paragraph 1 of these guidelines; and
    AF (m2)  

13 The maximum added resistance due to wind Xw is defined as maximum over wind directions from head ε=0 to 30 degrees off-bow ε=30.

14 The non-dimensional aerodynamic resistance coefficient is defined from wind tunnel tests or equivalent methods verified by the Administrations or the Recognized Organizations. Alternatively, it can be assumed with 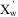= 1.1, as the maximum over wind directions from head to 30 degrees off-bow. If deck cranes are installed in the ship and the lateral projected area of the deck cranes is equal to or exceeds 10% of the total lateral projected area above the waterline of the ship, =1.4 should be assumed instead of =1.1.

Definition of added resistance due to waves

15 The maximum added resistance due to waves Xd is defined in accordance with either

  • .1 expression

    • Xd = 1336(5.3 + U)

    • where

    • Lpp (m) is the length of the ship between perpendiculars;
      B is the breadth of the ship;
      d is the draft at the specified condition of loading; and
      hs (m) This expression defines the maximum added resistance over wave directions from head to 30 degrees off-bow.

    • This expression defines the maximum added resistance over wave directions from head to 30 degrees off-bow.

  • .2 or spectral method

    • Xd = Sςς(ω′)D(μ−μ′) dω′ dμ′

    • where

    • is the quadratic transfer function of the added resistance in regular waves and A is the wave amplitude;
      Sςς(ω′) is the seaway spectrum specified as JONSWAP spectrum with the peak parameter 3.3;
      D(μ−μ′) is the spreading function of wave energy with respect to mean wave direction specified as cos2-directional spreading;
      ω′ (rad/s) is the wave frequency of component;
      μ (rad) is the encountered angle between ship and wave; and
      μ′ (rad) is the direction of the wave component.

16 The maximum added resistance due to waves Xd is defined as maximum over wave directions from head μ=0 to 30 degrees off-bow μ=30. The range of peak wave periods TP applied in the assessment is from 3.6 to the greater one of 5.0 or 12.0 seconds, with the step of peak wave period not exceeding 0.5 seconds.

17 The added resistance in short-crested irregular head waves may be regarded as the maximum added resistance over wave directions from head to 30 degrees off-bow, because in short-crested waves, the maximum added resistance over wave directions from head waves to 30 degrees off-bow occurs in head waves.

18 The spreading function D(μ−μ′) is defined as cos2-directional spreading. Alternatively, long-crested seaway may be assumed with D(μ−μ′) = 1; in this case, the maximum added resistance due to waves Xd can be determined by multiplying the added resistance in long-crested irregular head waves by the correction factor 1.3, to consider that maximum of the added resistance in long-crested waves does not always correspond to head wave direction.

19 The quadratic transfer functions of added resistance in regular waves are defined from seakeeping tests or equivalent methods verified by the Administrations or the Recognized Organizations. Alternatively, the semi-empirical method specified in appendix of this document can be used.

Definition of added rudder resistance due to manoeuvring in seaway

20 The maximum additional rudder resistance due to manoeuvring in seaway Xr may be calculated for practicality in a simplified way as

Xr=0.03 · Ter, where Ter is the propeller thrust excluding Xr from T.

APPENDIX TO APPENDIX 2 - SEMI-EMPIRICAL METHOD FOR QUADRATIC TRANSFER FUNCTIONS OF ADDED RESISTANCE IN REGULAR WAVES

The method for the calculation of the quadratic transfer functions of added resistance give in this appendix can be applied to wave directions from head to beam. Therefore, this method can be used for obtaining the added resistance in short-crested irregular waves of the head mean wave direction.

The quadratic transfer functions of added resistance in regular head to beam waves X′d=, N/m2, can be calculated as a sum

X′d = X′dM + X′dR

of X′dM, the component of added resistance due to motion (radiation) effect, and X′dR, the component of added resistance due to reflection (diffraction) effect in regular waves.

The expression of X′dM is given as follows:

where

for CB > 0.75 for CB ≤ 0.75

  • where

  • β= π − μ is the wave direction, β=π means head seas;
    λ (m) is the length of the incident wave;
    B (m) is the beam of the ship;
    d (m) is the draft of the ship; and
    kyy is the non-dimensional radius of gyration of pitch.

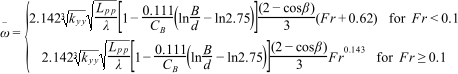
The expression of X′dR is given as follows:

where

  • is the added resistance due to reflection/diffraction effect of the Siwaterline segment, as shown in Figure 1.

  • Figure 1: Sketch of the waterline profile of a ship and related definitions

    when E1≤ β ≤ π

  • when π-E1 ≤ β ≤ π

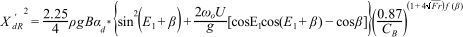
  • when 0 ≤ β ≤ π-E2

  • when 0 ≤ β ≤ E2

  • where

    • ω0 is the frequency of the incident wave;
      is the draft coefficient, calculated as

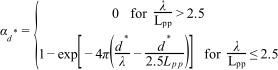
  • where for S1 and S2 segments

    • d* = d

    and for S3 and S4 segments

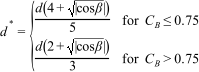
    f(β) =

Parent topic: MEPC.1/Circular.850 Rev.3 - Guidelines for Determining Minimum Propulsion Power to Maintain the Manoeuvrability of Ships in Adverse Conditions - (7 July 2021)
Copyright 2022 Clasifications Register Group Limited, International Maritime Organization, International Labour Organization or Maritime and Coastguard Agency. All rights reserved. Clasifications Register Group Limited, its affiliates and subsidiaries and their respective officers, employees or agents are, individually and collectively, referred to in this clause as 'Clasifications Register'. Clasifications Register assumes no responsibility and shall not be liable to any person for any loss, damage or expense caused by reliance on the information or advice in this document or howsoever provided, unless that person has signed a contract with the relevant Clasifications Register entity for the provision of this information or advice and in that case any responsibility or liability is exclusively on the terms and conditions set out in that contract.