6.1 Introduction

  6.1.1 The PIT technique is a general methodology for the determination of the numerical values for a certain number of parameters in a given analytical model, in such a way that the model can represent the physical behaviour of the system under analysis in the given conditions. Although the PIT technique is also suitable for the direct analysis of roll decays in calm water in order to obtain the ship natural frequency and the damping parameters, the roll motion of a ship in beam sea is dealt with in this document.

  6.1.2 The general idea on which the PIT is based is that the given analytical model is assumed to be able to predict the amplitude of roll motion of the ship in beam sea, and this model is characterized by a general form with a certain number of free parameters. The free parameters should be fixed in order to obtain the best agreement between available experimental data and numerical predictions from the model. When such parameters are determined, the model is assumed to be suitable for extrapolation. In the case of roll motion in beam sea, the model parameters is fit by using the ship roll response data for a small steepness in order to predict the ship behaviour at a larger steepness for which direct experiments cannot be carried out, or for which direct experiments are not available.

  6.1.3 The general equation assumed suitable for the modelling of roll motion in beam sea is, according to the Guidelines, the following:

  6.1.4 Where the following parameters are in principle to be considered as free (units are reported assuming the roll angle to be measured in radians):

  6.1.5 The wave steepness s, as well as the forcing frequency ω (to be measured directly from the roll time histories in order to account for Doppler effect if the drift speed is large), are given data from experiments.

  6.1.6 The total number of free parameters is, thus, in principle, equal to 9. Such a large number of parameters can be effectively determined from experimental data only when the number of experiments is large, i.e., at least two (but is better three) wave steepnesses leading to response curves spanning a large range of rolling angles from the linear range (below, say, 10°) up to the nonlinear range (say, at least 40°). In addition, experimental data should span a large range of frequencies from low to high frequency range (say, 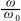from about 0.8 or lower to about 1.2 or higher). The necessity of spanning such a large domain is due to the fact that different parameters have a different importance in different ranges.

  6.1.7 While damping plays an important role mostly around the peak region, the effective wave slope is better determined if the low frequencies region of the response curve is also available. Linear terms in both damping and restoring are dominant in the region of small rolling amplitudes, while the effects of nonlinear terms are noticeable only in the region of large rolling amplitudes. 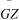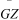The roll response curve tends to bend to the low frequency region when is of the softening type, and towards the high frequency region when is of the hardening type. Both type of bending could be noticeable when the righting lever is of the S-type.

  6.1.8 The general use of the PIT in the framework of the experimental determination of the roll angle φ _1r (See the Guidelines) will likely to be similar to that of the Three steps procedure, i.e. as follows:

• .1 carry out experiments at a single steepness s _exp smaller than the required one s _req;

• .2 determine model parameters in order to fit the experiments at s _exp;

• .3 utilize the obtained parameters in order to predict the peak of the ship roll response at s _req;

  6.1.9 Since only one steepness is likely to be available, the number of parameters should be reduced in order to achieve convergence of the methodology without spurious effects on undetectable parameters. A reduced model is then to be used.

  6.1.10 On the bases of a series of studies and on the experience gained in the past (see, e.g., [1][2]), the following reduced model can be proposed when only one steepness is available:

1 steepness reduced model:

where the damping has been considered to be purely quadratic due to the fact that only one amplitude response curve is available. The frequency dependence of the effective wave slope has been dropped because we are mainly interested in this context in the ship response at peak, and so the tails are of less (or none) importance for the final evaluation of φ _1r (even if the low frequency tail of the roll response is fundamental for the fitting of the value of α ₀). As a note, the coefficient α ₀ in the reduced model (N-6.2) corresponds to the effective wave slope "r" of the Three Steps Procedure. A cubic nonlinear restoring term has been kept, but it can be removed if the 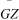curve is sufficiently linear in the expected response range, or if there is no evidence of bending from the experimental response curve (provided the experimental peak is sufficiently large to allow the identification of the possible nonlinear behaviour).

  6.1.11 In the case where two response curves are available determined at two different steepnesses, it is possible to introduce an additional linear damping term and an additional 5th degree restoring term:

2 steepness reduced model:

  6.1.12 Regarding the damping term in the previous reduced models, in general the quadratic damping component seems to be more suitable for the analysis of hulls with bilge keels or with an expected large vortex generation. On the other hand, the substitution of the quadratic term 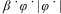with a cubic term 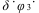could be more suitable for bare hulls.

  6.1.13 The use of different nonlinear damping models, can lead to different results in the prediction of the final rolling amplitude. For this reason, in the absence of sufficient evidence for the selection of one nonlinear model versus the others, the use of the average of the two predicted peak rolling amplitudes is recommended. A pure linear model, on the other hand, is almost always inadequate for the representation of roll damping at zero speed.